 Source: Wikipedia
Source: Wikipedia
Imagine you start with a perfectly ordinary equilateral triangle
- The Little Triangle Trick
- Take each side of your big triangle and chop it into three equal pieces.
- On the middle piece, stick out a smaller, pointy triangle—like giving your triangle a little hat.
- Boom! One straight side just turned into four zig-zag segments.
-
Repeat Forever (or Until Bedtime)
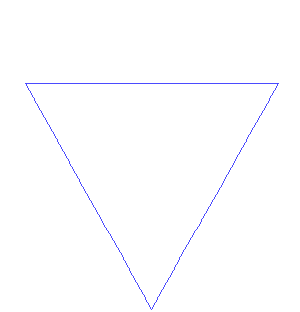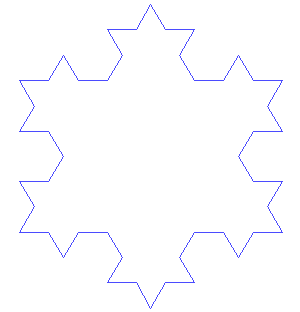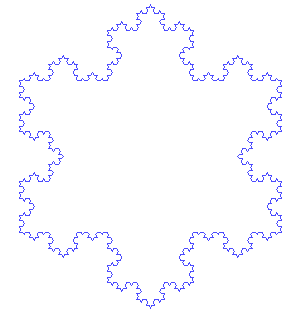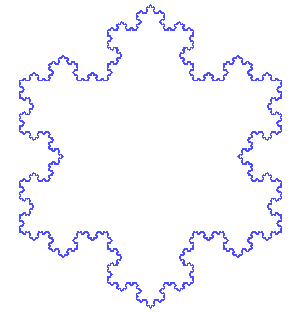
Do the same “chop-and-hat” dance on every straight segment you have, again and again. After a handful of rounds, that once-smooth triangle looks like a lacy, frosty snowflake—except it never truly finishes growing.
- Why It’s So Cool
- Endless Coastline Vibes: The boundary keeps getting longer, like a coastline that never stops.
- Finite Snowball: Even though its edge stretches off toward infinity, the area inside tops out at a nice, finite size.
- Fractal Antennas
In real world, I leared Koch Snowflake is useful for Antennas design. Those jagged edges pack loads of “wire” into a small footprint—perfect for some application like phones, Wi-Fi routers, and satellites.

Source: Miniaturization of a Koch-Type Fractal Antenna for Wi-Fi Applications
Swedish mathematician Helge von Koch published a short note to give a simple example of a curve that is continuous everywhere, but differentiable nowhere—challenging the then-prevailing intuition that most “nice” curves should have well-defined tangents at almost every point.
Now let’s play the draw a Koch Snowflake at different orders , using Python below:
Notes: Because Google Colab cannot display Turtle window, need to use your local editor, for example Jupyter Notebook, to show the animation
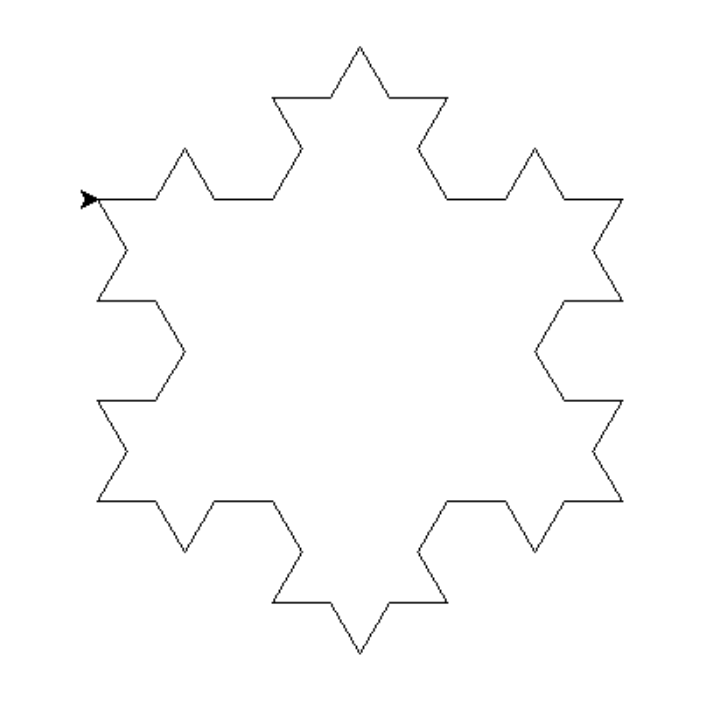
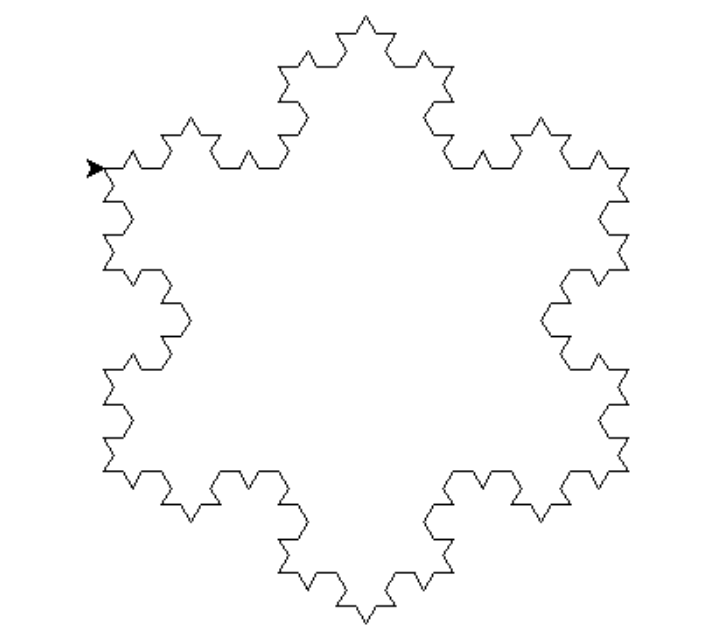
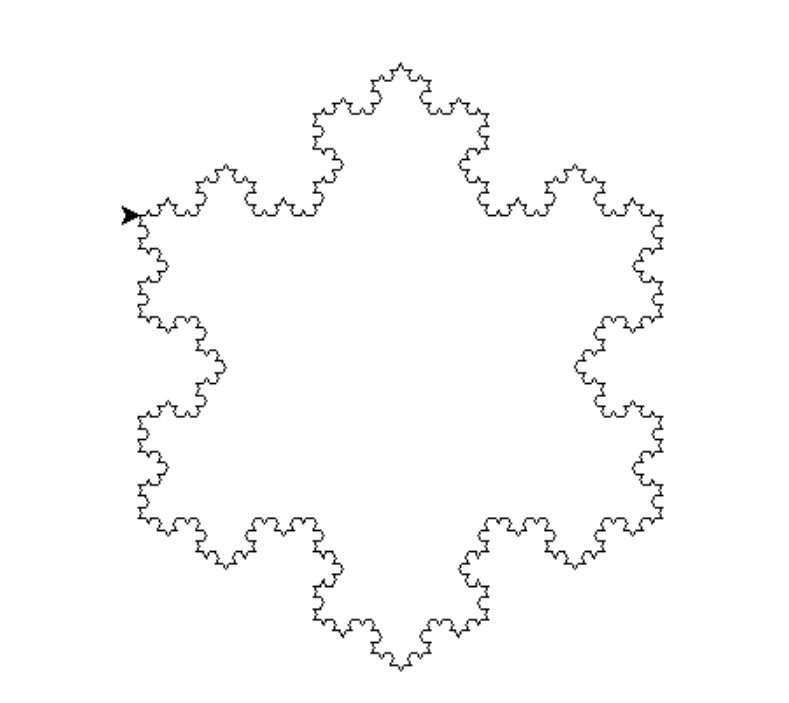
Leave your comments below!
Python Code
import turtle
def koch_curve(t, order, size):
if order == 0:
t.forward(size)
else:
for angle in [60, -120, 60, 0]:
koch_curve(t, order - 1, size / 3)
t.left(angle)
def koch_snowflake(t, order, size):
for _ in range(3):
koch_curve(t, order, size)
t.right(120)
if __name__ == '__main__':
screen = turtle.Screen()
screen.bgcolor("white")
t = turtle.Turtle()
t.speed(0) # Set speed to fastest
t.penup()
t.goto(-150, 100) # Adjust starting position
t.pendown()
order = 2 # Set the order (recursion depth)
size = 300 # Set the size of the snowflake
koch_snowflake(t, order, size)
screen.mainloop()