In the 3rd century, Chinese mathematician Liu Hui Wikipeida approximated π, by inscribing regular polygons in a circle and letting the number of sides double.
Let’s recreate his method in Python!


Play with the code, by changing the “n” variables in the code below,
either at my google colab page.
What is the Collatz?
- Pick any positive integer (n).
- If it’s even, divide it by 2:
[
n \;\to\;\frac{n}{2}
]
- If it’s odd, multiply by 3 and add 1:
[
n \;\to\;3n + 1
]
- Repeat.
Once you hit 1, the “3×+1” rule sends you back into the loop
[
1 \to 4 \to 2 \to 1
]
forever—like reaching the checkered flag in an infinite race.
What is the Collatz map?
A German mathematician named Lothar Collatz[Wikipeida] (https://en.wikipedia.org/wiki/Collatz_conjecture) posed a simple question:
“What happens if we repeatedly apply this 3n+1 rule to any positive integer?”
Every number he tried eventually reached 1, and proposed this might be true for all numbers. Despite how easy it sounds, no one has ever proven it—it remains one of the biggest unsolved puzzles in math!
A “Collatz map” shows the correlation of any integer and it eventually envolved into 1!
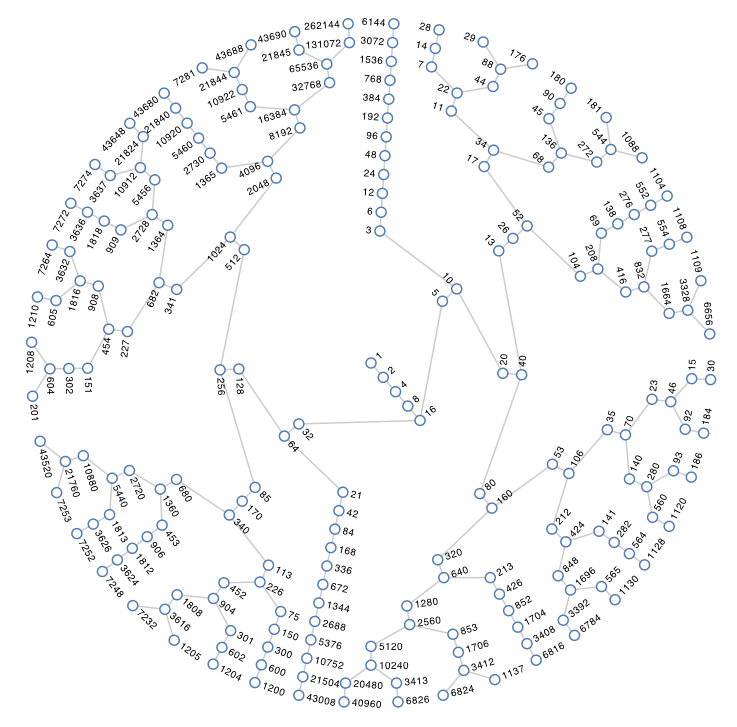
Why spiral?
Goes from Collatz map, and plot each integer around a growing spiral, then draw an arrow from each $n$ to its next Collatz iterate, you get a breathtaking web of curves that really spiral around the center. With Python code, one can visulization based on Collatz conjecture.
The “Collatz spiral” is plotted by taking each term of a Collatz sequence and embedding it in polar (and then Cartesian) coordinates.
1. Collatz Map
Define the Collatz map (C(n)) by
\[C(n) =
\begin{cases}
\displaystyle \frac{n}{2}, & \text{if $n$ is even},\\[6pt]
3n + 1, & \text{if $n$ is odd}.
\end{cases}\]
Starting from a seed integer (s_0), generate the sequence
\[s_{k+1} = C(s_k), \quad k = 0,1,2,\dots\]
2. Polar Embedding
For each term (s_k), set
\(r_k = s_k,
\qquad
\theta_k = \ln(s_k).\)
You may optionally multiply (\ln(s_k)) by a constant factor to tighten or loosen the spiral.
3. Cartesian Coordinates
Convert ((r_k,\theta_k)) into ((x_k,y_k)) via
\[\begin{aligned}
x_k &= r_k \cos(\theta_k) = s_k \cos\bigl(\ln s_k\bigr),\\
y_k &= r_k \sin(\theta_k) = s_k \sin\bigl(\ln s_k\bigr).
\end{aligned}\]
Putting it all together, the plot of the first (N) terms is
\[(x_k,y_k) = \bigl(s_k\cos(\ln s_k),\;s_k\sin(\ln s_k)\bigr),
\quad
k=0,\dots,N.\]
Where (s_0) is your chosen starting integer and (s_{k+1} = C(s_k)).
Before the in-depth study of fractal geometry, artists in 16th-century such as lace-makers and stone-carvers created repeating self-similar patterns and created artwork with it. A notable example is the Sierpinski’s Triangle:
source


Interestingly, the Sierpinski’s triangle also appears naturally:
